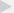行测技巧:细数古典型概率的一二三
 查字典公务员网
查字典公务员网
概率问题是历年国考行测的常考点,而其中的古典型概率是概率问题中最关键以及最重要的考点之一。同时,古典型概率往往会与排列组合的知识点结合考察。那今天教育专家就跟大家来一起看看,如何在考试中拿下古典型概率吧。
一、什么是古典型概率
在了解古典型概率之前,我们先行回忆一下概率的概念,它无非就是描述一件事情发生的可能性大小,它的取值范围一定是介于0到1之间的。

根据古典型概率的基本概念,我们可以发现,试验中出现的结果一定是有限个,而事件A所包含的结果发生的可能都是一样的。也就是说,古典型概率必须满足两个条件:a)有限性;b)等可能性。因此,解决古典型概率的关键就在于找到试验中产生的结果n值和事件A包含的结果m值,而找n和m的方法就有多种了,那我们一起来看看可以通过哪些方式解决问题。
二、古典型概率的考察形式
1.枚举
题干中的n和m可以直接根据题干信息逐一枚举出来。
【例1】某单位共有4个部门,部门一为12人、部门二为15人、部门三为20人、部门四为23人,抽1人参加培训学习活动,抽到部门三的概率为( )。

直接通过枚举的方式找n和m的题型相对来说比较简单,相比而言我们更需要重点学习通过排列组合来寻求n和m值,并且求得概率的考题。
2.排列数和组合数
题干中的n和m需要通过排列或组合的方法求出来。
【例2】某单位端午节3天假期安排甲、乙、丙、丁4人值班。端午节当天上、下午各安排一个人值班,另外两人每天安排一个人,每人只值班一次。则乙被安排在端午节当天值班的概率是()

排列组合寻找m和n值的时候,一定不能遗漏每个部分的方法数,所以排列组合的知识点也要掌握得很到位,才能很好的处理好概率问题。
3.间接求
当题目中出现相较比较复杂的概率计算时,直接计算会发现计算比较复杂,但是我们却发现所计算部分的对立面(即A事件不发生的概率)相对更容易计算,那我们就可以通过1-P(对立面)来计算A发生的概率。题目中往往出现至少字眼的时候,考虑间接计算。
【例3】一个办公室有2男3女工5个职员,从中随机挑选出2个人参加培训,那么至少有一个男职员参加培训的概率为()

教育专家认为概率问题并非难点,只要找到m和n的值,问题就很好解决,特别需要注意在用排列组合解决概率问题时,要注意不可遗漏方法数。相信各位考生可以通过对各类题型的充分练习更好地掌握古典型概率这个知识点,并且在考试过程中拿下分数。



 返回首页
返回首页