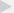剩余问题

2008-10-26 04:10:07

查字典公务员网

剩余问题

在我国古代算书《孙子算经》中有这样一个问题：今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？意思就是，一个数除以3余2，除以5余3，除以7余2。求适合这个条件的最小数？

类似于这个问题的题目，我们称之为剩余问题。

在《孙子算经》中给出了它的一种解法：三三数之，取数七十，与余数二相乘；五五数之，取数二十一，与余数三相乘；七七数之，取数十五，与余数二相乘。将诸乘积相加，然后减去一百零五的倍数。列式计算就是：702＋213＋152=233，233大于105的2倍210，则所求最小的数就是233-1052=23。其中，70、21、15分别是从3、5、7的最小公倍数357=105中分别除以3、5、7再乘以相应的整数2、1、1得到的。而70、21、15分别除以3、5、7，余数都是1。

在明朝时，数学家程大位把这一解法编成四句歌诀：

三人同行七十（70）稀，五树梅花廿一（21）枝，

七子团圆正月半（15），除百零五（105）便得知。

在公务员的考试中，也有类似的试题出现。除了使用这种基本方法外，有些题目也有自己的性质，可以采取一些特别的方法。

例1：某数除以11余8，除以13余10，除以17余12，那么这个数的最小可能值是（）

A.140 B.569 C.712 D.998

解析：这道题的三个数分别相乘的结果比较大，都大于100；而三个数的公倍数则超过2000千，因此，用《孙子算经》来解计算量是很大的。

11-8=3，13-10=3，则要求的这个数加上3后，可以被11和13整除，则它加上3后是11和13的最小公倍数1113=143的倍数，检验四个选项，发现四个选项都符合该条件。另外一个已知条件就是，这个数应该加上17-12=5后被17整除，只有D项的998满足答案。据此，可排除A、B、C。

正确答案：D

例2：１个数除５余３，除６余４，除７余１，这样的３位数有几个？

解答：5、6、7的最小公倍数是567=210，且1000210=4160，则满足题意的3位数有4个或5个。当满足条件的最小的数是一个三位数且它小于160时，答案就是5；否则，答案就是4。即当一个数a满足题意时，a+210n（n=0，1，2，）也满足题意。

证明如下：

（a+210n）5=a5+42，则该余数与a除以5的余数相同。

同理可得a+210n除以6、7的余数分别与a除以6、7的余数相同。

则a+210n和a除以5、6、7的余数都是相同的。

由于5-3=2，6-4=2，则这个数加上2以后，可以被5、6整除，即可以被5、6的最小公倍数30整除，即该数=30n+28（n=1，2，3，）。又因为该数除以7余1，而28是7的4倍，则30n应该除以7余1，而307=42，且24=8=7+1，则（304）7=171，则最小的满足条件的数就是304+28=148，是一个三位数。

（a+210n）5=a5+42，则该余数与a除以5的余数相同。

同理可得a+210n除以6、7的余数分别与a除以6、7的余数相同。

则a+210n和a除以5、6、7的余数都是相同的。

这样，满足题意的三位数就是148，148+210=358，148+2210=568，148+3210=568=778，148+4210=988，一共有5个。

例3：篮子里装有不多于500个苹果，如果每次二个、每次三个、每次四个、每次五个、每次六个地取出，篮子中都剩下一个苹果，而如果每次七个地取出，那么没有苹果剩下，篮子中共有多少个苹果？

A.298 B.299 　 C.300 D.301

解析：由题目可知，答案应该能被7整除，四个选项中，只有D符合这个条件。

另外，苹果的总数应该是2、3、4、5、6的公倍数再加1，且能被7整除。2、3、4、5、6的最小公倍数是60，则苹果总数就是60n+1(n=1，2，3，)。

60n+1应该是7的整数倍，607=84，则60n+1=78n+4n+1，即4n+1是7的倍数，用7的1、2、3倍试算，当4n+1=73=21时，n=5时满足条件的最小值，则60n+1=301。满足条件的数就是301。

正确答案：D

例4：一支队伍不超过6000人，列队时，2人一排，3人一排，4个一排直至10人一排，最后一排都缺一个人。改为11人一排，最后一排只有1个人。问这一队伍有多少人？

A.4926人 B.5039人 C.5312人 D.5496人