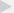行测：突破固定模式，巧解行程问题

公务员考试行测部分中的数学运算一直是广大考生朋友非常头疼的问题，常感觉无处下手，头脑中根本就没有解题思路。其实，考试中的这一部分题目运算过程比较简单，并不需要高深的数学知识，但要求思路灵活、能找全题目中的所有可用条件、并能熟练运用各数量间关系。这些题目可以分为很多类型，每种类型都有固定的、可套用的解题方法。我们将其一一总结出来，并加以细致分析，最后熟练掌握之后，在考试中就可以顺利解答了。数学运算中解题思路最广、方法最灵活的就是行程问题了。

行程问题基础知识

行程问题中的相遇问题和追及问题主要的变化是在人（或事物）的数量和运动方向上。我们可以简单的理解成：相遇（相离）问题和追及问题当中参与者必须是两个人（或事物）以上；如果它们的运动方向相反，则为相遇（相离）问题，如果他们的运动方向相同，则为追及问题。

相遇（相离）问题的基本数量关系：

速度和相遇时间=相遇（相离）路程

追及问题的基本数量关系：

速度差追及时间=路程差

在相遇（相离）问题和追及问题中，我们必须很好的理解各数量的含义及其在数学运算中是如何给出的，这样才恩能够提高我们的解题速度和能力。

例1

甲、乙两人联系跑步，若让乙先跑12米，则甲经6秒追上乙，若乙比甲先跑2秒，则甲要5秒追上乙，如果乙先跑9秒，甲再追乙，那么10秒后，两人相距多少米？

A.15 B.20 C.25 D.30

【答案】C。解析：甲乙的速度差为126=2米/秒，则乙的速度为252=5米/秒，如果乙先跑9秒，甲再追乙，那么10秒后，两人相距59－210=25米。

例2

兄弟两人早晨6时20分从家里出发去学校，哥哥每分钟行100米，弟弟每分钟行60米，哥哥到达学校后休息5分钟，突然发现学具忘带了，立即返回，中途碰到弟弟，这时是7时15分。从家到学校的距离是多少米？

A.3500 B.3750 C.4150 D.4250

【答案】C。解析：哥哥50分钟走一个来回，弟弟55分钟走一个来回，故一个单程为（10050+6055）2=4150米。

例3

一艘轮船从河的上游甲港顺流到达下游的丙港，然后调头逆流向上到达中游的乙港，共用了12小时。已知这条轮船的顺流速度是逆流速度的2倍，水流速度是每小时2千米，从甲港到乙港相距18千米。则甲、丙两港间的距离为（ ）

A.44千米 B.48千米 C.30千米 D.36千米

【答案】A。解析：顺流速度－逆流速度=2水流速度，又顺流速度=2逆流速度，可知顺流速度=4水流速度=8千米/时，逆流速度=2水流速度=4千米/时。设甲、丙两港间距离为X千米，可列方程X8+（X－18）4=12 解得X=44。

深刻理解路程、时间、速度的关系，巧妙解题

速度的单位一般为米/秒、米/分、千米/时等，代表的是在单位时间内走过的路程，代表的是一种线性的路程和时间的关系。这里应注意单位时间其实是可以人为规定的，相当于方程里面设未知数为X，那么路程和速度也相对的被人为规定了，比如某人在一段时间内走过了10千米，那么他在10倍这段时间内就走过了100千米。能够灵活的运用这种关系，对于理解题目和简化计算过程都非常有好处。以下题为例：

一只游轮从甲港顺流而下到乙港，马上又逆水返回甲港，共用8小时，顺水每小时比逆水每小时多行12千米，前4小时比后4小时多行30千米。甲、乙两港相距多少千米？

A.72 B.60 C.55 D.48

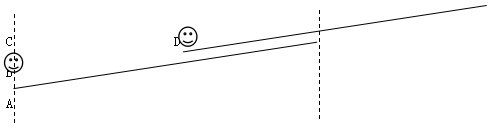
解析：在这个题目中出现了前4小时比后4小时多行30千米，把4个小时的路程作为了一个标准路程，那么应该怎样理解呢这句话呢？首先我们来看一下前4个小时走过的路程和后4个小时走过的路程都代表了什么。画路程图如下，BC=CD。

众所周知，船在顺水中的速度一定大于在逆水中的速度，那么在整个行程的8个小时中，前4个小时一定是该船顺水到达乙港后，又逆水走了一段路程所用的时间，即前4个小时走过了AB+BC，后4个小时就只是逆水到达甲港所用的时间，即后4个小时走过了CA。现在将两段路程相减，AB+BC－CA=AB－DA=30公里。此时大家可以想象一下，AB为顺水走过的路程，DA呢？是否等于在相同时间内逆水走过的路程？当然答案是肯定的。由AB－CD=30，我们就可以求出顺水行驶过AB的时间为3012=2.5小时，那么逆水行驶了8－2.5=5.5小时。又AB－DA=BD=30公里，那么逆水的速度也可以求得，30（8－2.5－2.5）=10公里，则甲、乙两港相距105.5=55公里，此题选择C。

希望通过这道例题，可以让大家了解到在相同时间内走过的路程在行程问题中的重要性。并能找到适当的切入点，灵活运用这种关系，横扫行程问题。